SimplicityTheory

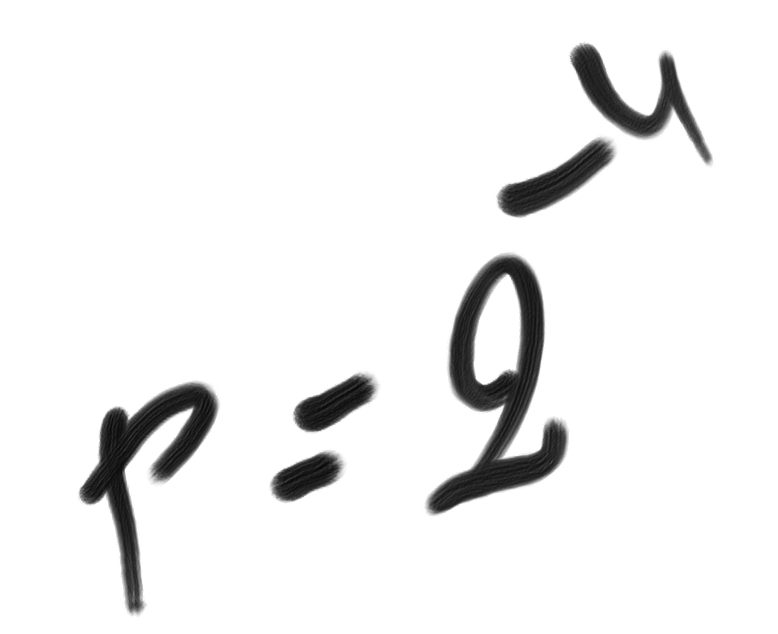Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information

The ‘Rabid Bat’ effect (generation complexity)

THE BAT STORY

"There is one in ten million chance of getting bitten by a rabid bat. So, I’m not curious, but I would really like to know how the guy managed to estimate that we have ALL - on average - one chance in ten million of getting bitten. Yes, because well... Myself, I’m living in the 10th district [of Paris]. Well, first, the 10th district, where bats are concerned, it’s a quite calm place, one must admit. What’s more, I’m living five floors up without a lift, I’ll tell you, there is a digital lock at the entrance door and an entry phone. Ha, ha ! So, I’ll tell you, the bat can always turn up, you see ! So, but ok, suppose it does. A bat arrives. A rabid one. (...) So... Hop ! It starts tinkering with my code. It’s there, tinkering. It tries, it tries. (...) Pan ! It hits on the right code ! It still needs to imitate the voice of a guy I know !!! Otherwise, I won’t open ! (...) Well ! It reaches my floor ... What proves that it will knock at MY door? There’re four apartments on the floor..." © JEAN-MARIE BIGARD / PIERRE PALMADE

By definition, unexpectedness U is the difference between generation complexity and description complexity: C_w – C. An event that is complex to generate (large C_w) will appear more unexpected. It will therefore appear more improbable, thanks to the formula p=2^–U.
You may appreciate the accumulation of details aiming at increasing generation complexity C_w. The target situation (Bigard getting bitten by a rabid bat) is difficult to generate in the known world, since:

♦    there are few bats in the 10th district of Paris
Bringing one rabid bat by chance to Bigard’s building is difficult. Various computations of C_w are possible (bat-centred or building-centred). They all end up with: C_w = log₂ B₁ – log₂ B₂ + constant, where B₁ and B₂ represent the number of buildings and the number of bats in the 10^th district. Note that the ‘constant’ includes the logarithm of the proportion of rabid bats in the bat population. Note also that the mention of the 10th district (a homogeneous, densely populated district) aims at increasing the difference log₂ B₁ – log₂ B₂ (but it is "paid" on the complexity side, C; therefore, the authors do not mention "I am living in the south-west part of the 10^th district").

♦    there are many combinations for the digital lock
Finding the right combination by chance amounts to log₂ C₁, where C₁ is the number of combinations.

♦    it is difficult for a bat to imitate the voice of one of Bigard’s friends
Here, there are two sources of high generation complexity: the rabid bad is not supposed to know Bigard’s friends (hence a term in log₂ V₁ where V₁ is the total number of recognizable voices); and even in the alternative reality that is already installed, bats are not supposed to be very good at imitating human voices.

♦    there are four apartments on the floor
This adds two bits to C_w.

We could push the analysis even further (why the 10^th district and not the 1^st one?; why mentioning the absence of lift...). The point is that in the absence of a model of how the world works (e.g. that climbing stairs is tiring, therefore higher motivation is required to climb further up...), there is no chance to understand the funny aspects of the story. Conversely, any proper assessment of C_w is sufficient here to understand why the event (Bigard getting bitten by a rabid bat) is highly improbable.

Moreover, the difference C_w - C provides a strict relevance criterion for the story. For instance, Bigard does not mention that the entrance door is blue, as it would have no bearing on C_w and would unnecessarily increase C.

Bibliography

Dessalles, J-L. (2013). Algorithmic simplicity and relevance. In D. L. Dowe (Ed.), Algorithmic probability and friends - LNAI 7070, 119-130. Berlin, D: Springer Verlag.

Back to the Simplicity Theory page.