SimplicityTheory

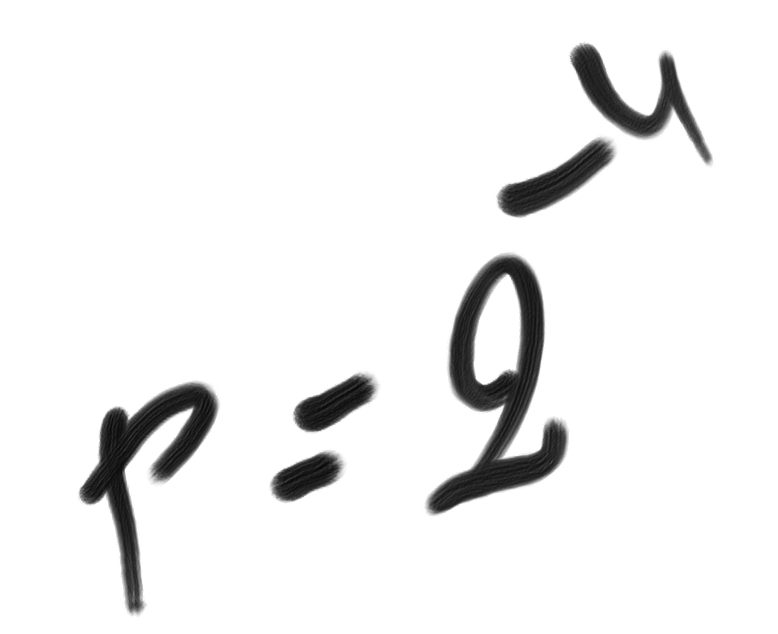Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information


by Jean-Louis Dessalles     (created 31 December 2008, updated March 2020)

Simplicity and Emotion

Simplicity Theory was initially designed to account for the interestingness of events. It was obvious that both emotional intensity and complexity played crucial roles in determining the value of events (e.g. their newsworthiness). Less obvious was the fact that this two contributions were to be considered on an equal foot.

Emotional intensity and complexity can be converted one into the other.
A famous example is provided by what French journalists call la loi du mort-kilomètre (the casualty/mile law). For similar dramatic events to get the same newsworthiness, the most distant ones must involve more victims, as if the ratio of the number of casualties over the distance (or rather the square of the distance) had to remain constant. The greater the distance, the more complex the event; this added complexity must be compensated by more emotion (more victims).

Hypothetical emotion

Let’s call Eh(s) the emotional term contributing to the interestingness of an event s, together with unexpectedness. Eh(s) captures the fact that, all or other things being equal, an event involving the death of people will be more emotional than if it involved the death of, say, dogs or mice. We write that the emotional intensity E(s) attached to event s as:

E(s) = Eh(s) + U(s).

The term Eh(s) is called hypothetical emotional intensity. Actual emotional intensity E(s) results from the contribution of Eh(s) and of from the unexpectedness U(s) of s.

We may write :

Eh(s) = E(s) – U(s)     (if E(s) > U(s)).

If we convert unexpectedness into subjective probability through formula p = 2–U, Eh(s) can be interpreted as a logarithmic version of the expected value.[Note]
Eh(s) could, in principle, be measured by some kind of insurance procedure: how much money would you pay to make s impossible (for a negative eventuality) or to prevent s from being impossible (for a positive eventuality).

A purely epistemic situation is characterized by the fact that Eh(s) = 0. One does neither wish nor fear the occurrence of s. However, the occurrence of s might be still be surprising, due to the term U(s).
When Eh(s) ≠ 0, the situation is said to be epithymic.

Emotions

Simplicity Theory says nothing about the quality of emotions. It deals with the intensity of emotions as far as they are reportable.

The (reportable) emotional intensity attached to a situation s is noted E(s). The positive or negative aspect of emotions is called valence. We write:

e(s) = ε(s) E(s)

where e(s) represents the emotional strength and ε(s) is the valence of event s.

The falling roof tile

How do we receive a story like this one?

-->

I rent a ground floor flat and park my car in a specified parking place. Last Sunday (after some fairly strong overnight winds) I noticed that a couple of tiles had come off the roof of the flat above me and one had hit and damaged my car.

The story is not purely epistemic. It has an emotional (epithymic) component that any car owner can feel.
Let’s call s(ego, now) the situation of "discovering that one’s car was hit by a fallen roof tile" and E(s(ego, now)) the emotional intensity attached to that situation. The corresponding hypothetical emotion can be computed as:

Eh(s) = E(s(ego, now)) – U(s(ego, now)).


Let’s call s(x, t) the situation "x had her car hit t days ago by a fallen roof tile". The problem is to compute E(s(x, t)). We can write:

E(s(x, t)) = Eh(s) + U(s(x, t)).

This expression shows how emotional intensity depends on unexpectedness. In particular, the high value of the causal complexity is a crucial ingredient of the story.

In this story, we may assume that the causal complexity of the event does not depend on the victim. From the expression of unexpectedness, we may rewrite the preceding expression, considering that C(ego, now) = 0 and that C(s(x, t)) = C(s) + C(x) + C(t):

E(s(x, t)) = Eh(s) + U(s(x, t)) = E(s(ego, now)) – C(s) – C(x) – C(t).

The story is more emotional if it recently happened (C(t) small) to a close acquaintance (C(x) small), and if the conceptual content of the story ("car hit by a fallen roof tile") is already in the context (C(s) = 0).

Bibliography

Dessalles, J.-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications. (Chapitre 4)

Dessalles, J-L. (2010). Emotion in good luck and bad luck: predictions from simplicity theory. In S. Ohlsson & R. Catrambone (Eds.), Proceedings of the 32nd Annual Conference of the Cognitive Science Society, 1928-1933. Austin, TX: Cognitive Science Society.

Dessalles, J-L. (2011). Simplicity Effects in the Experience of Near-Miss. In L. Carlson, C. Hoelscher & T. F. Shipley (Eds.), Proceedings of the 33rd Annual Conference of the Cognitive Science Society, 408-413. Austin, TX: Cognitive Science Society.

Saillenfest, A. & Dessalles, J-L. (2012). Role of kolmogorov complexity on interest in moral dilemma stories. In N. Miyake, D. Peebles & R. Cooper (Eds.), Proceedings of the 34th Annual Conference of the Cognitive Science Society, 947-952. Austin, TX: Cognitive Science Society.

Saillenfest, A. & Dessalles, J-L. (2014). Can Believable Characters Act Unexpectedly?. Literary & Linguistic Computing, 29 (4), 606-620.

Saillenfest, A. & Dessalles, J.-L. (2015). Some probability judgments may rely on complexity assessments. Proceedings of the 37th Annual Conference of the Cognitive Science Society, 2069-2074. Austin, TX: Cognitive Science Society.

    

___________________________

[Note] Note, however, that unexpectedness corresponds to ex post probability while mathematical probability is restricted to ex ante anticipation (Saillenfest & Dessalles, 2015).

Back to the Simplicity Theory page.