SimplicityTheory |
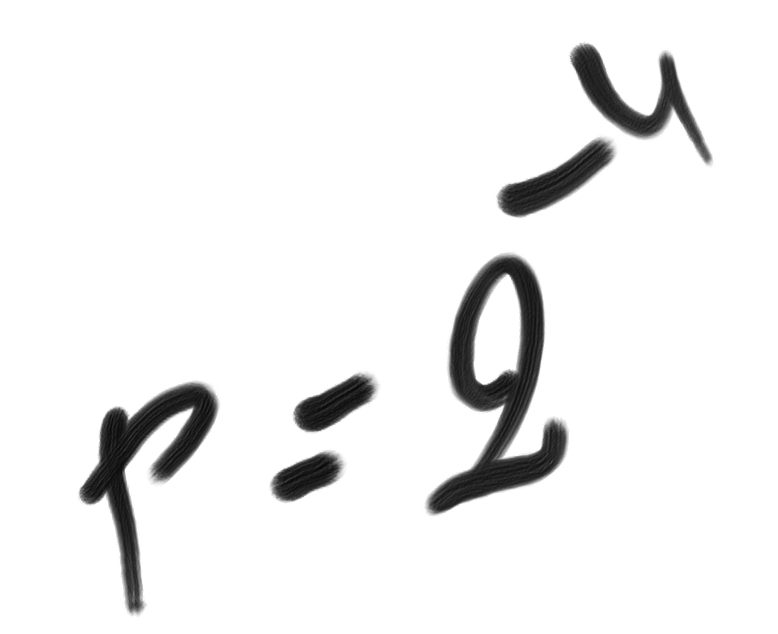 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)
Remarkable structures - The Lottery example
Simple structures seem unexpected. |
Though all lottery combinations have equal probability, individuals judge simple combinations to be much less likely (Savoie & Ladouceur 1995; Dessalles, 2006). According to Simplicity Theory, this is due to the fact that lottery draws that appear simple are judged unexpected.
By definition, unexpectedness U is the difference between generation complexity and description complexity: Cw – C. Let’s compute both terms.
Generation complexity Cw
 The generation complexity of lottery drawings is always about 6 × log2 49, if six numbers are drawn among 49 (in fact a little less, as a number cannot been drawn twice).
The generation complexity of lottery drawings is always about 6 × log2 49, if six numbers are drawn among 49 (in fact a little less, as a number cannot been drawn twice).
Description complexity C
Description complexity of lottery draws depends on their structure. The following table shows description complexity estimates for various combinations, based on an application of Leyton’s generative theory of shape (see (Dessalles, 2006) for details).
Combinations |
Complexity | Probability |
|
1 2 3 4 5 6 34 35 36 37 38 39 10 11 12 44 45 46 7 8 9 37 38 39 8 9 26 27 28 29 10 20 30 31 32 33 1 2 5 6 15 49 . . . 14 24 36 38 42 44 |
3 |
p/8 × 10^6 p/10^6 p/32768 p/16384 p/16384 p/16384 p/4096 . . . p |
The description complexity depends on the structure the subject is able to detect in the combination.
Similarly, when a child sitting in a car sees 66666 on the clock, she can’t help drawing the driver’s attention to the event. Generating such a number requires five instantiations (complexity = 5 × log2 10) whereas its description requires only one instantiation and one iterated copy (complexity = log2 10 + Ccopy). If we neglect the complexity of copying, formula p=2–U gives a subjective probability of 10–4, which explains the child’s behaviour.
Note that the definition of probability p=2–U conflicts with traditional definitions to be found in complexity theory (Solomonoff 1997), for which simple objects are more likely. Solomonoff’s definition, however, pays attention only to generation complexity and not to description complexity. This is why it makes wrong predictions in the case of Lottery draws.
Bibliography
Dessalles, J.-L. (2006). A structural model of intuitive probability. In D. Fum, F. Del Missier & A. Stocco (Eds.), Proceedings of the seventh International Conference on Cognitive Modeling, 86-91. Trieste, IT: Edizioni Goliardiche.
Saillenfest, A. & Dessalles, J.-L. (2015). Some probability judgments may rely on complexity assessments. Proceedings of the 37th Annual Conference of the Cognitive Science Society, to appear. Austin, TX: Cognitive Science Society.
Savoie, D. & Ladouceur, R. (1995). Évaluation et modification de conceptions erronées au sujet des loteries. Canadian Journal of Behavioural Science, 27 (2), 199-213.
Solomonoff, R. J. (1997). The discovery of algorithmic probability. Journal of Computer and System Sciences, 55 (1), 73-88.
![]()