SimplicityTheory |
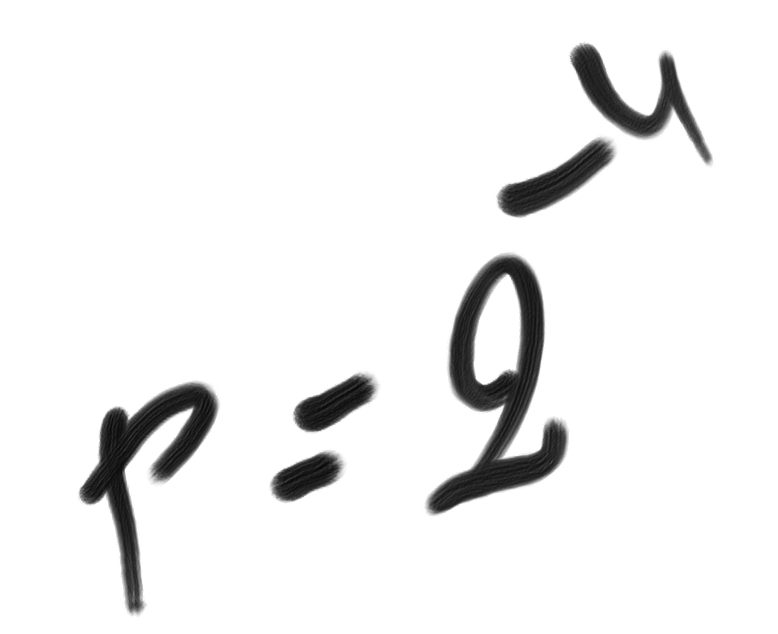 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)
The "Robert Wadlow" effect (record)
Extremes are unexpected because they are simple in their class. |
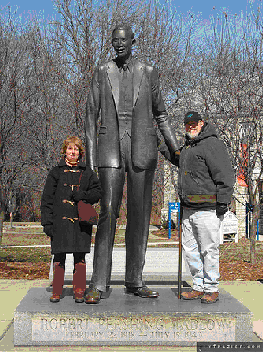
Robert Pershing Wadlow is thought to be the tallest man in human history.
His size (2,72m) made him well-known in the USA and around the world.
Extreme situations or objects are unexpected. Why and how much?
By definition, unexpectedness U is the difference between generation complexity and description complexity: Cw – C.
Generation complexity Cw
Suppose you consider the extreme object, situation or person b as member of a reference class r. In R. Wadlow’s example, r may be the class of human beings, the class of men, the class of tall men, the set of all men you ever encountered, etc. If b is considered as randomly drawn from r (i.e. feature f (here the extreme size) has no causal effect on b being chosen), then:
Cw(b|r) = log2 N
where N is the number of elements in class r. This is because the "world-machine" needs log2 N bits to discriminate among all elements in r which one it will present to you (for details, see the Inverted Stamp example).
Description complexity C
Feature f may be used as the best way to discriminate b in class r. Therefore:
C(b|r) = C(f) + C(b|r&f)
If b is thought to be unique in its kind, then C(b|r&f) = 0. We get:U(b|r) = log2 N – C(f)
Finally, if r is not itself unexpected (i.e. Cw(r) = C(r)):U(b) = log2 N – C(f) – C(r)
The corrective term C(f) accounts for the fact that records must be kept as simple as possible for unexpectedness to remain meaningful. Some recorded achievements are borderline in this respect: "Fastest speed while swapping places on a motorcycle", recorded on the 2003 edition of the British edition of the Guinness book, requires a more complex description than "Fastest motorcycle speed" or "Earliest bicycle", listed on the same page.
Bibliography
Dessalles, J.-L. (2007). Spontaneous assessment of complexity in the selection of events. Technical Report ParisTech-ENST 2007D011.
Dessalles, J-L. (2008). Coincidences and the encounter problem: A formal account. In B. C. Love, K. McRae & V. M. Sloutsky (Eds.), Proceedings of the 30th Annual Conference of the Cognitive Science Society, 2134-2139. Austin, TX: Cognitive Science Society.
Dessalles, J-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications.
Dimulescu, A. & Dessalles, J-L. (2009). Understanding narrative interest: Some evidence on the role of unexpectedness. In N. A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society, 1734-1739. Amsterdam, NL: Cognitive Science Society.
![]()