SimplicityTheory

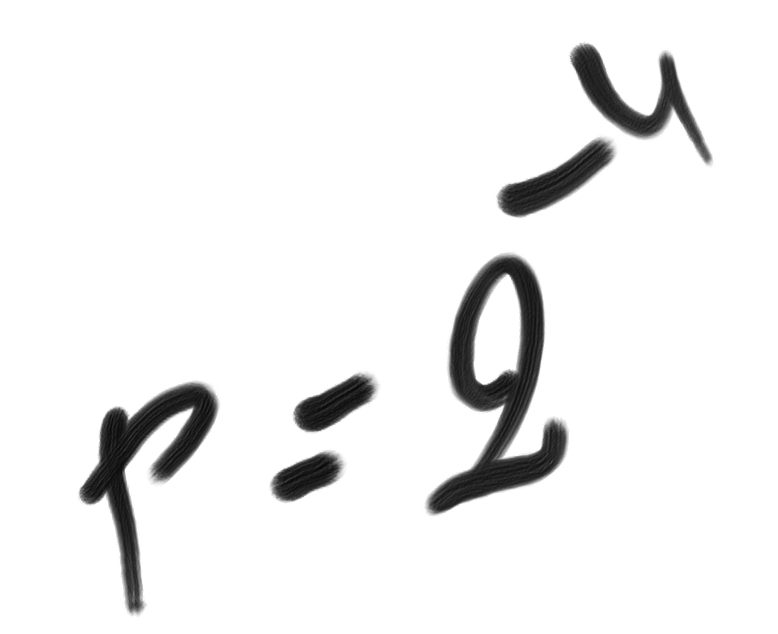Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information

by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)

The "Eiffel Tower" effect (landmark)


Prominent places are simple and make events more unexpected.

Consider the prominence of places. A man jumps from a hotel window. News? Yes, but vastly more so if he leaps from the top of the Eiffel Tower, the Washington Monument, the Statue of Liberty or Niagara falls. An event in an ordinary house is less likely to see print than an event in the White House. Monte Carlo, the Riviera, Death Valley, Hollywood, Las Vegas, Miami Beach, the Loop, the Golden Triangle, Times Square, Broadway and the Bowery are further examples of places instantly recognized or imagined by everyone. (Warren 1934/1959:21)

22 July 2003: a minor blaze in an electrical cabinet at the third floor of the Eiffel Tower was reported in the national news.

Events happening close to prominent places are more unexpected and thus more newsworthy. Why? And how much more?

By definition, unexpectedness U is the difference between generation complexity and description complexity: C_w – C.

Description complexity C

The computation of description complexity may go through the computation sequence L*x, where L is a prominent landmark and x is the location of the unexpected situation (event). We may write:

C(x) < C(L*x) = C(L) + C(x|L)

The computation of C(x|L) is the same as for the "next door effect". Simply, the distance d_L to the landmark is used instead of egocentric distance. We get:

C(x|L) = log₂(πd_L²/a)

where a is the area of the event itself. More generally, if the event occurred within a spatiotemporal volume v_L centred on L, then the complexity of x relative to L amounts to:

C(x|L) = log₂ (v_L/v_x)

As in the "next door effect", C_w(x) = log₂ (V_e/a). We eventually get:

U(x) > log₂ (V_e/v_L) – C(L)

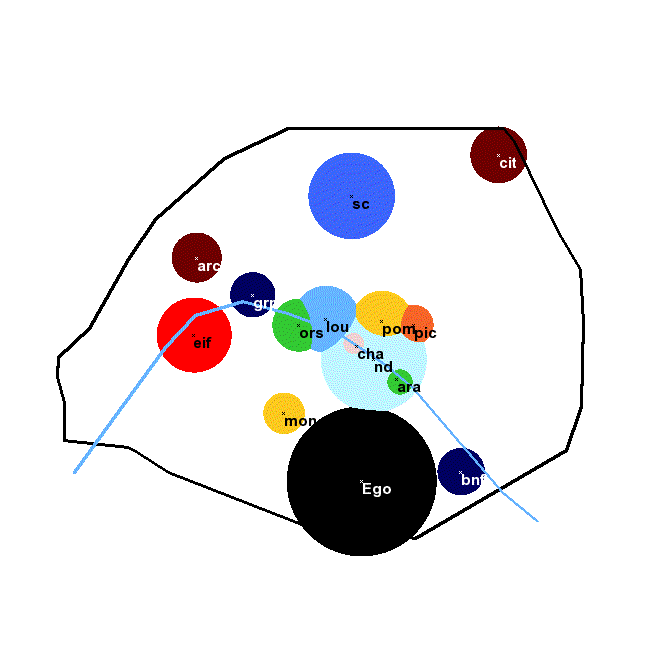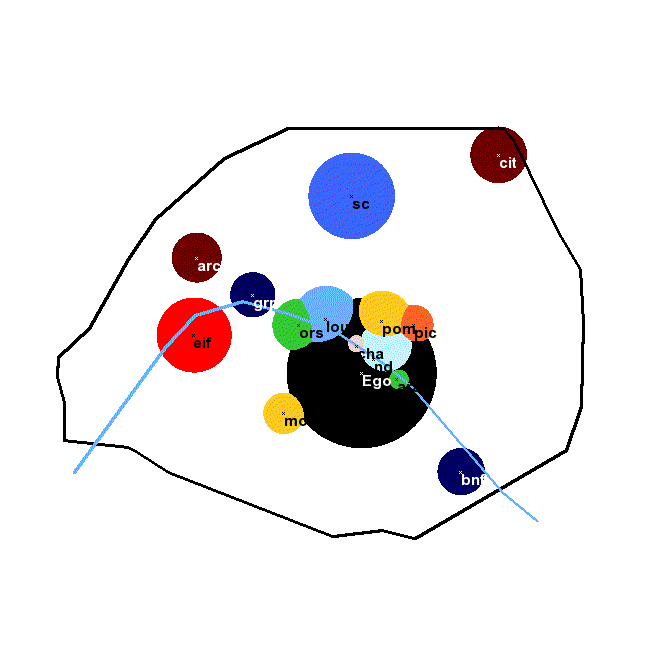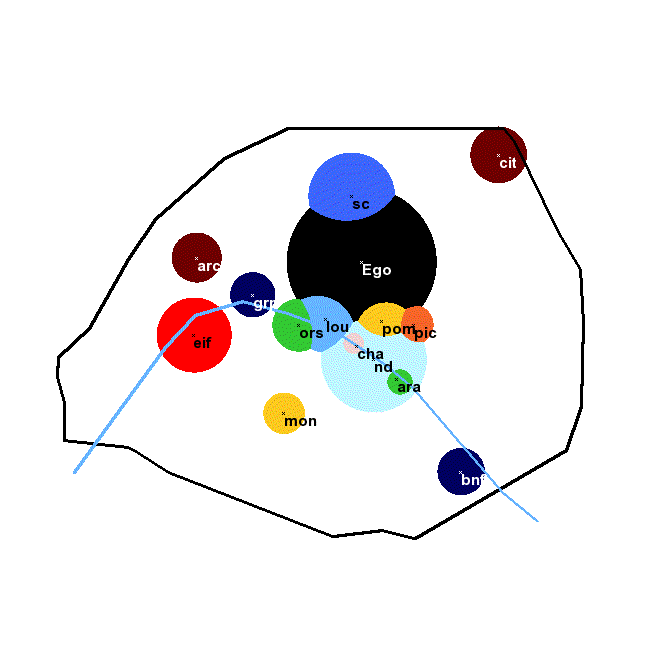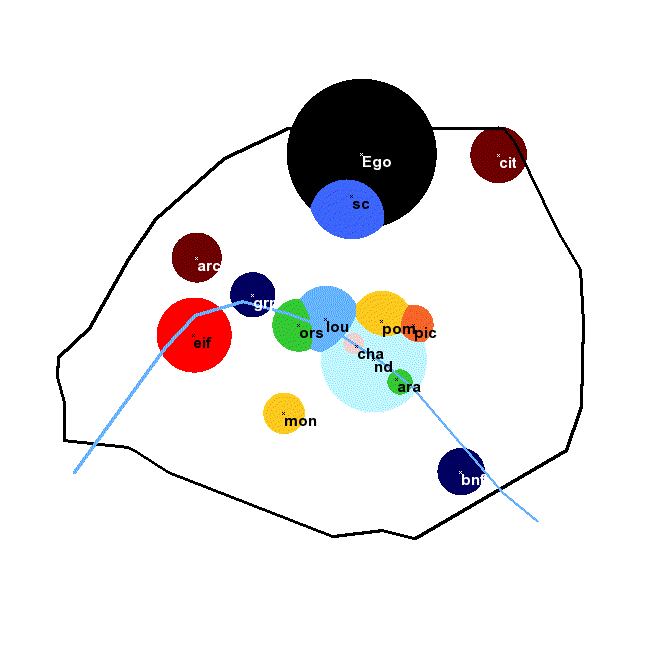
This formula predicts when a landmark will be used, and which landmark will be chosen if there are several available ones. The best spatial landmark in two dimensions, L₀, makes C(L) + 2 × log(d_L) minimum:

L₀ = argmin[ C(L) + 2 log₂(d_L) ]

ego can be included in the set of candidate landmarks, with complexity equal to zero. In two dimensions, landmarks behave like Newtonian attractors, as their influence on improbability (through formula p=2^–U) decreases as the square of the distance to them. Their area of influence varies like 2^–C(L).

The picture below shows a map of Paris with the main monuments ranked according to the number of tourist visits. Each monument would be used by a tourist as a landmark within the zone of corresponding colour. The influence of a monument diminishes as log₂ r (where r is the rank of the monument in the list) and twice the logarithm of the distance to the point. The largest zone is the ego zone in black (displayed in successive positions if you see it moving). Outside the coloured zones, no landmark is used except the city of Paris itself.

Bibliography

Dessalles, J.-L. (2007). Spontaneous assessment of complexity in the selection of events. Technical Report ParisTech-ENST 2007D011.

Dessalles, J-L. (2008). Coincidences and the encounter problem: A formal account. In B. C. Love, K. McRae & V. M. Sloutsky (Eds.), Proceedings of the 30th Annual Conference of the Cognitive Science Society, 2134-2139. Austin, TX: Cognitive Science Society.

Dessalles, J-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications.

Dimulescu, A. & Dessalles, J-L. (2009). Understanding narrative interest: Some evidence on the role of unexpectedness. In N. A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society, 1734-1739. Amsterdam, NL: Cognitive Science Society.

Back to the Simplicity Theory page.