SimplicityTheory |
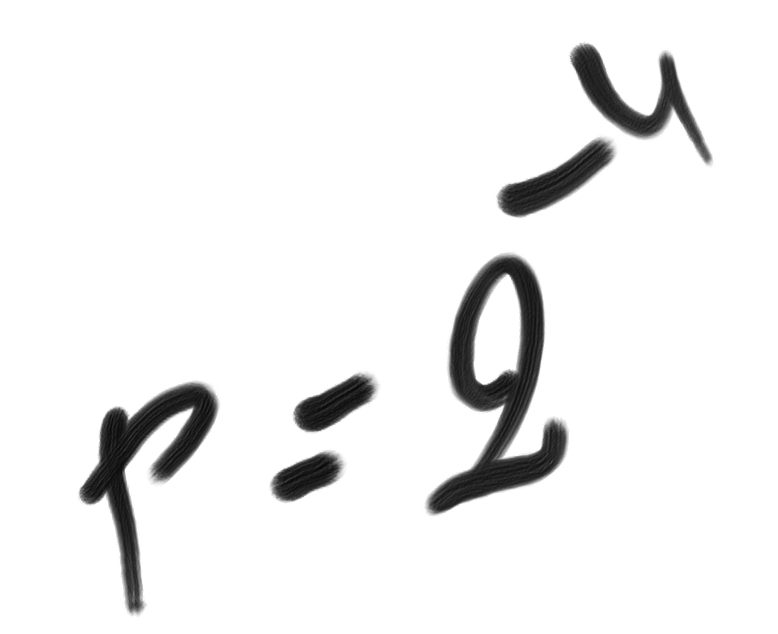 |
Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information
by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)
The Fish story effect (atypicality)
Atypical elements are unexpected because they are simple in their class. |
Atypical situations or objects are unexpected. Why and how much?
By definition, unexpectedness U is the difference between generation complexity and description complexity: Cw – C.
Generation complexity Cw
Suppose you consider the object b (e.g. a big mushroom) as member of a reference class r (r may be the class of mushrooms). If the quantitative feature f (here the large size) has no causal effect on b being considered, then:
Cw(b|r) = log2 N
where N is the number of elements in class r. This is because the "world-machine" needs log2 N bits to discriminate among all elements in r which one it will present to you (for details, see the Inverted Stamp example).
Description complexity C
Feature f may be used as the best way to discriminate b in class r. Therefore:
C(b|r) = C(f) + C(b|r&f)
With a negligible added complexity, objects in r can be ranked according to the quantitative feature f (remember that complexity only cares about the size of algorithms, not about their execution time). Object b will be one of the firsts in this ranking. We may write: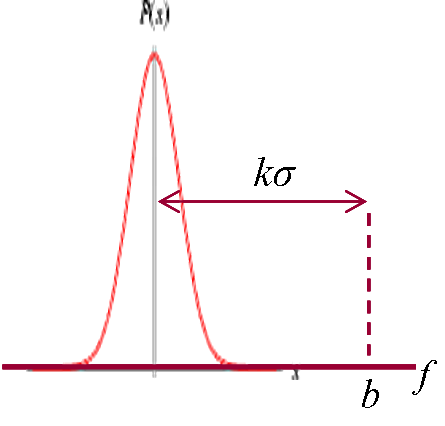
C(b|r&f) = log2 N – A(k)
where k is the number of standard deviations of b in the f-distribution of r. A(k) is the logarithm of the number of objects in r that are beyond k standard deviations for f. For a Laplace-Gauss distribution, we have A(k) ≈ 0.72 k2 + log2 k + 1.33 (for k > 1). The preceding relation holds as long as A(k) < log2 N. Beyond that, the atypical object becomes unique; it is perceived as a record or an impossibility.Finally:
U(b|r) = A(k) – C(f)
and (since Cw(r) = 0 if r-object are supposed to exist):U(b) = A(k) – C(f) – C(r)
The corrective terms C(f) accounts for the fact that only simple atypical features make objects rare. The Louisiane crayfish (Procambarus clarkii) is atypical because it has as many as 200 chromosomes; this fact will seem unexpected to a geneticist, for whom the feature is simple, but a layman may remain stonily indifferent as the complexity of the feature consumes most of the complexity drop due to atypicality.
Procambarus clarkii
Bibliography
Dessalles, J.-L. (2007). Spontaneous assessment of complexity in the selection of events. Technical Report ParisTech-ENST 2007D011.
Dessalles, J-L. (2008). Coincidences and the encounter problem: A formal account. In B. C. Love, K. McRae & V. M. Sloutsky (Eds.), Proceedings of the 30th Annual Conference of the Cognitive Science Society, 2134-2139. Austin, TX: Cognitive Science Society.
Dessalles, J-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes-Science Publications.
Dimulescu, A. & Dessalles, J-L. (2009). Understanding narrative interest: Some evidence on the role of unexpectedness. In N. A. Taatgen & H. van Rijn (Eds.), Proceedings of the 31st Annual Conference of the Cognitive Science Society, 1734-1739. Amsterdam, NL: Cognitive Science Society.
![]()

