SimplicityTheory

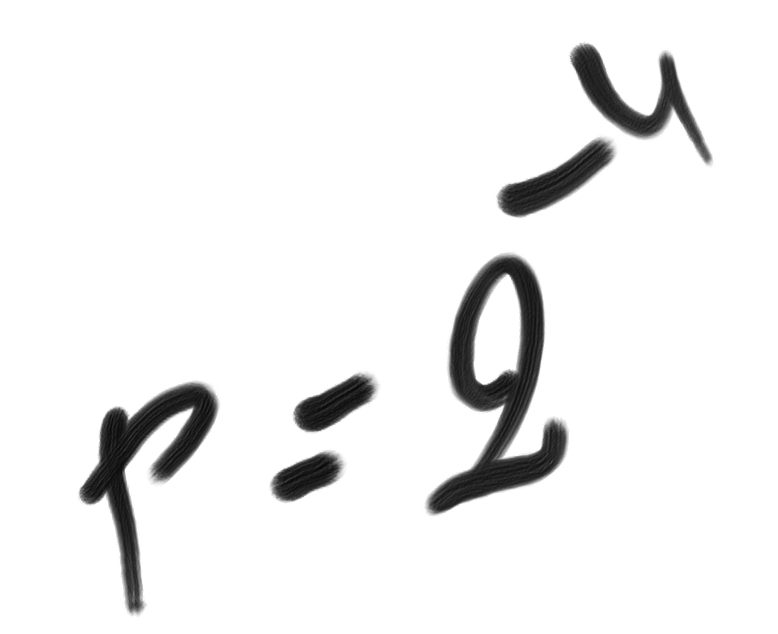Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information

by Jean-Louis Dessalles (created 31 December 2008, updated March 2020)

Simplicity, Intention, moral judgments and responsibility

Intention

We consider an action a performed by A that had consequence s.
Did A perform a intentionally?

Simplicity Theory defines intention as the global necessity of the action from the actor’s perspective.

A’s intention to do a can be written as the cumulative effect of different necessity sources:

Simplicity Theory defines intention as the global necessity of the action from the actor’s perspective.

I(A, a) = ∑ ν_i^A(a).

where the ν_i^A(a) are the different necessity values of a computed from A’s perspective. In the simple cas in which a has only one emotional consequence s which A values with intensity E^A(s), we can write:

I(A, a) = E^A(s) – C_w^A(s|a) – U^A(a).

Superscripts ^A indicate that all computations are done from A’s perspective.
- note that all terms are assessed by the observer who has to adopt A’s perspective.
- note that when ¬a (i.e. not performing a) has emotional consequences, they should be taken into account as well; see the definition of necessity.
- note that all computations in this formula are supposed to have taken place ex ante, before the action took place.

We can see that:

intention increases with the importance of the outcome.
intention diminishes with the uncertainty of the causal link, as measured by conditional causal complexity C_w(s|a).
intention diminishes with inadvertence U(a)

Moral judgments and responsibility

Consider again an action a performed by A that had consequence s.
Is A to be blamed or praised for having done a?

In the framework of Simplicity Theory,

the moral judgment about an action amounts to the necessity of the action where the observer’s values are substituted for the actors’s values.

When a has only one emotional consequence s, the intensity of the moral judgment M(A, a) ascribed by the observer O to A’s action a can be written as (Saillenfest & Dessalles, 2012):

the moral judgment about an action amounts to the necessity of the action where the observer’s values are substituted for the actors’s values.

|M(A, a)| = E^O(s) – C_w^A(s|a) – U^A(a). (valid only if > 0).

Superscripts ^A indicate computations that are done from A’s perspective. Superscript ^O will be omitted and considered implicit.
- note that though M(A, a) and I(A, a) may coincide if O and A share the same emotions, M(A, a) is computed ex post, after the fact, whereas I(A, a) is supposed to have been computed ex ante.
- note that to be blamed or praised from O’s perspective, A should have anticipated the causal link from action a to O’s emotional response. The two terms C_w^A(s|a) + U^A(a) with superscript A capture the legal notion of mens rea. The fact that computations are ascribed to the actor explains why in most cultures, small children or animals causing dammage may not be blamed for it (see however the unfortunate fate of elephant Mary).

Using the definition of hypothetical emotion E_h and the definition of unexpectedness, we can rewrite the preceding definition.

|M(A, a)| = E_h(s) – C(s) + (C_w(s) – C_w^A(s|a)) – U^A(a).

We introduce two new notions:

Causal responsibility: R(A, a, s) = C_w(s) – C_w^A(s|a).
Inadvertence: F(A, a) = U^A(a).

We get (for a single outcome s): |M(A, a)| = E_h(s) – C(s) + R(A, a, s) – F(A, a).
or, in shorter form:

|M| = E_h – C + R – F

Blame or praise increases with the stakes E_h.
Blame or praise diminishes with the complexity of the event C(s). Suppose that s involves a victim who is close to O (C(s) small). O’s moral judgment will be more intense.
Blame or praise increases with causal responsibility R.
Blame or praise diminishes when the action has been performed inadvertently.

The following story explores a situation in which actions have several consequences.

The tunnel story

The following story is a modified version of the classical trolley problem (Thomson, 1985).

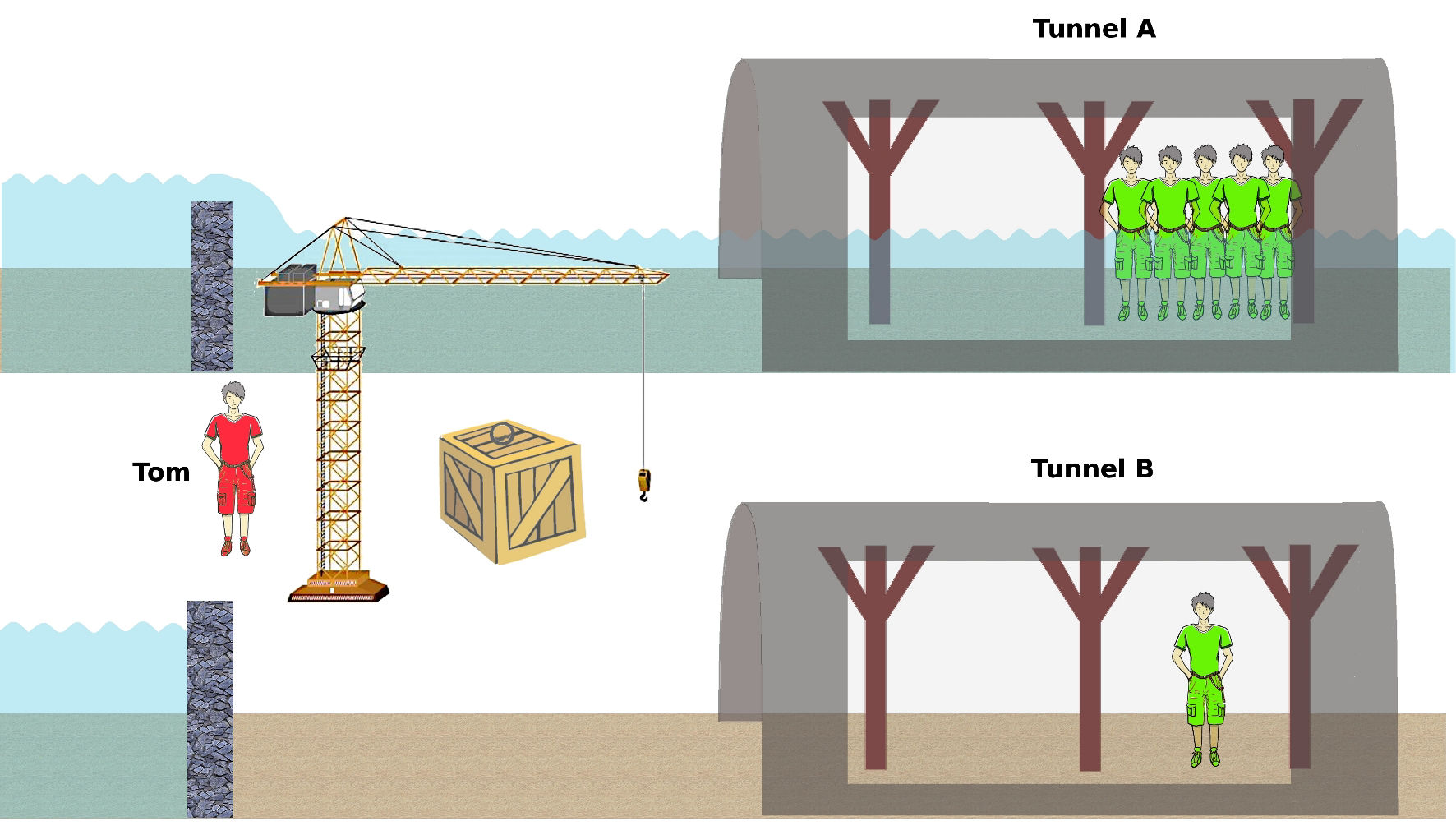
Tom works in a mine in Argentina. As he was watching the river upstream from the mining site, he could observe a sudden rise in the water level. He instantaneously understood the danger. One of the two tunnels of the mine was about to get flooded. Tom knew that there were five people in this tunnel (tunnel A). In the other tunnel (tunnel B), there was only one person. The water level was rising fast. The trapped persons were going to drown.
Tom stood at the entrance of the two tunnels, near a crane and a heavy and voluminous box. He knew he could not interrupt the current in both tunnels, but he could divert the current from one tunnel into the other. He also knew that he was the only person who could do anything at this point.

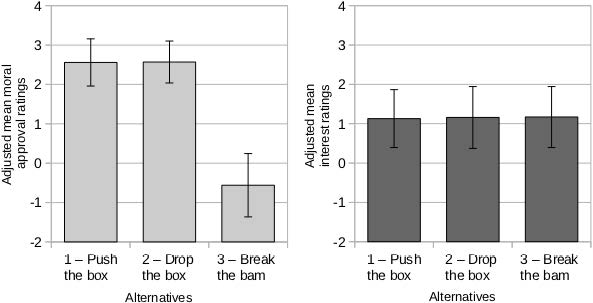
There are three versions for this story.


Tom pushed the box in front of the entrance of the tunnel A in order to interrupt the current in this tunnel. Tom got in the crane, grabbed the box with the crane’s hook, brought the box above the entrance of the tunnel A and dropped it in the middle of the current to stop the current in the tunnel. Tom broke the dam of tunnel B to flood this tunnel immediately. As a consequence, the water level stopped rising in tunnel A, but tunnel B got flooded. Five persons were saved, one person died by drowning	(Saillenfest & Dessalles, 2012)

Though the outcome is the same in each case, moral approval is lower in (3).

Interpretation

We can apply the definition of moral judgment. In a dilemma situation, however, action a has two emotional effects, and non-action ¬a has emotional consequences as well. The necessity of action a is computed by taking all emotional consequences into account together with their ********** NO ACTION for l0 on Emotion.html,Valence. Since Tom’s actions are purposeful, we ignore the inadvertence term.

On the positive size (five saved that would have died if non-action): ν⁺(a) = (E(¬death5) – C_w(¬death5|a)) + (E(death5) – C_w(death5|¬a)) On the negative size (one person dead that would have been safe if non-action): ν^–(a) = –(E(death1) – C_w(death1|a)) – (E(¬death1) – C_w(¬death1|¬a)) We may suppose E(¬death5) = 0 and E(¬death1) = 0 (normal situation).
We also knwow that non-action leads to the death of five people (C_w(death5|¬a) = 0) and one person safe (C_w(¬death1|¬a) = 0).
We get the expression of the moral dilemma:

M(Tom, a) = [E(death5) – C_w(¬death5|a)] – [E(death1) – C_w(death1|a)]

When Tom blocks tunnel A, we can consider that his action has a direct effect on saving the five miners and an indirect effect on the death of the isolated miner: C_w(¬death5|a) << C_w(death1|a). In this case, judgment about a is positive.

When Tom breaks the dam of tunnel B, we have the converse situation: C_w(¬death5|a) >> C_w(death1|a). This may prove sufficient to reverse the judgment.

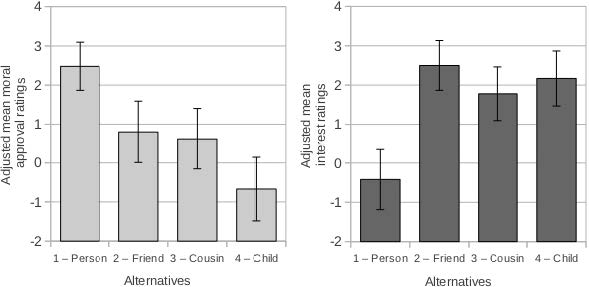
We may add another condition to the story.

Tom knew that [X] was in tunnel B. Tom pushed the box in front of the entrance of tunnel A.
It interrupted the current in tunnel A, tunnel B was flooded.
Five persons were saved, [X’] died.
where [X / X’] is:
someone / one person

one of his friends / Tom’s friend

his own cousin / Tom’s cousin

a 10-years old child / the child

(Saillenfest & Dessalles, 2012)
Moral approval is lower when Tom knows the victim, and lowest in the child condition.
Note that the story is considered more interesting when the audience disapprove of Tom’s action.

Tom knew that [X] was in tunnel B. Tom pushed the box in front of the entrance of tunnel A. It interrupted the current in tunnel A, tunnel B was flooded. Five persons were saved, [X’] died. where [X / X’] is: someone / one person one of his friends / Tom’s friend his own cousin / Tom’s cousin a 10-years old child / the child	(Saillenfest & Dessalles, 2012)

Interpretation

The victim’s identity affects the terms E_h(death1) – C(death1) in the expression of the moral judgment, either by increasing E_h(death1) (child condition) or by diminishing C(death1) (friend/cousin condition).

Bibliography

Dessalles, J.-L. (2008). La pertinence et ses origines cognitives - Nouvelles théories. Paris: Hermes Science.

Saillenfest, A. & Dessalles, J.-L. (2012). Role of kolmogorov complexity on interest in moral dilemma stories. In N. Miyake, D. Peebles & R. Cooper (Eds.), Proceedings of the 34th Annual Conference of the Cognitive Science Society, 947-952. Austin, TX: Cognitive Science Society.

Saillenfest, A. & Dessalles, J.-L. (2014). Can Believable Characters Act Unexpectedly?. Literary & Linguistic Computing, 29 (4), 606-620.

Saillenfest, A. (2015). Modélisation cognitive de la pertinence narrative en vue de l’évaluation et de la génération de récits. Paris: Thèse de doctorat -2015-ENST-0073.

Sileno, G., Saillenfest, A. & Dessalles, J.-L. (2017). A computational model of moral and legal responsibility via simplicity theory. .

Thomson, J. J. (1985). The Trolley Problem. The Yale Law Journal, 94 (6), 1395-1415.

Back to the Simplicity Theory page.