Simplicity Theory


SimplicityTheory

Simplicity, Complexity, Unexpectedness, Cognition, Probability, Information

by Jean-Louis Dessalles (created 31 December 2008, updated February 2026)

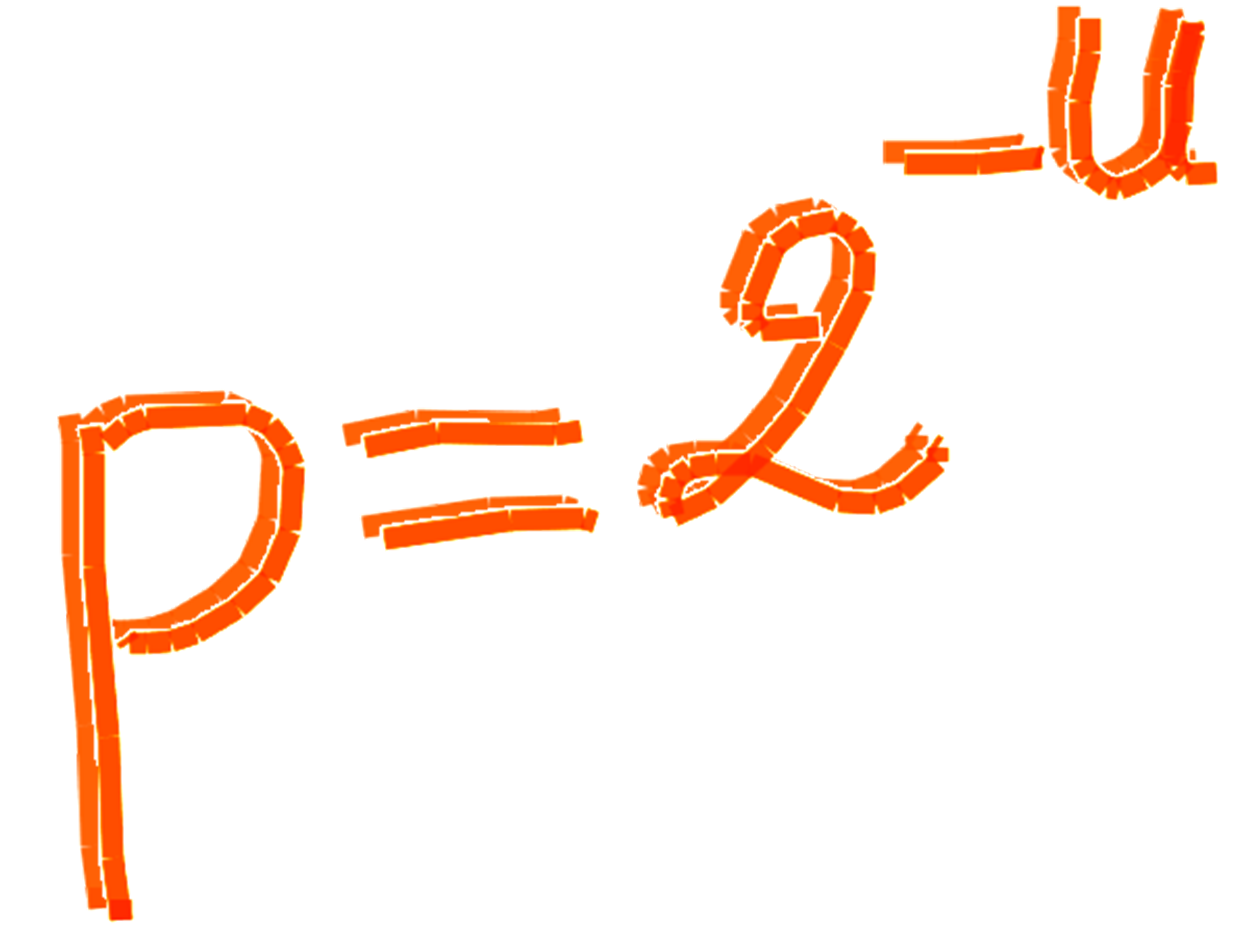
Simplicity Theory (ST) is a cognitive theory based on the following observation:
human individuals are highly sensitive to any discrepancy in complexity.
Their interest is aroused by any situation which appears "too simple" to them.

This has consequences for the computation of


(narrative) Interest	Relevance	Emotional Intensity.

ST’s central result is that Unexpectedness is the difference between expected complexity and observed complexity.
One important consequence is the formula p = 2^-U, which states that ex post probability p depends,
not on complexity, but on unexpectedness U, which is a difference in complexity.

Context

Finding out what elicits human interest is a fundamental scientific question which, quite surprisingly, has not been given much scientific attention in past decades. This is unfortunate, given that:

Our species is unique in what draws the attention of its members. For instance, only human beings are amazed at coincidences.
Much in human social relationships depends on shared interests, unlike what is to be observed in other species.
A considerable part of modern economies is devoted to eliciting interest through films, books, shows, media and games.

The scientific study of the determining factors of human interest may have been hindered by the tacit assumption that these factors are way too complex, multiple and fuzzy to be properly modelled. The results presented in these pages were obtained thanks to the converse assumption: our minds would be much simpler than commonly believed. Ironically, simplicity plays a major role in the theory presented here. Our minds seem to possess the amazing ability to monitor the complexity of some of their own processes. Here, complexity has to be taken in its technical acceptation (size of minimal description).

These pages are an invitation to challenge the model they present. All suggestions, critiques and contributions are welcome. Please send reactions to JL at@ dessalles.fr.

Significance for language and cognitive sciences

ST provides a formal and predictive model that impacts on the following domains:

relevance in spontaneous language and in the news (what is interesting, and what is appropriate to say)
high-level salience (what will attract my attention)
subjective probability judgements (decision, regret, some so-called "biases" in probabilistic reasoning)
emotion intensity (amplification through unexpectedness)

Simplicity Theory (ST)

*ST’s main claim*
An event is unexpected if it is simpler (=less complex) to describe than to generate.

All terms are important here.

Event: Event means unique situation (not classes of objects nor sets or whatever). We perceive plenty of unique situations, often characterized by the four Ws (When, Where, What, Who).
Complex: Complexity refers to the size of the minimal unambiguous description (see below).
Simpler: Simplicity is the amount of a complexity drop.
Describe: Since we are dealing with unique situations, the problem of a description is to produce that uniqueness. It can be achieved through a description of some characteristics of the situation that allow to isolate the situation from its class; it can also be achieved thanks to spatiotemporal determination.
Generate: Events are not any combination of disparate items. They were produced, generated, by the "world" (or some world, e.g. in fiction). Generation complexity is the minimal description of the parameters that have to be set for the "world" to generate the situation.
Unexpectedness is one of the two ingredients of interest (the other being emotional intensity). Unexpectedness, properly defined, predicts what will be considered interesting in human communication, e.g. in conversational narratives and in the news. It also predicts the kind of situations that will draw human attention.

Formally:

*ST’s main claim*
Unexpectedness: U = C_w – C

U: unexpectedness
C_w: generation complexity (= size of the minimal description of parameters values the "world" needs to generate the situation)
C: description complexity (= size of the minimal description that makes the situation unique)

Generation complexity C_w(s) is the complexity (minimal description) of all parameters that have to be set for the situation s to exist in the "world". For example, the complexity of generating the fact that you reach me by chance, knowing that you have to cross five four-road junctions to do so, is 5 × log₂ 3 = 7.9 bits.

We may consider C_w(s) as the length of a minimal program that the "W-Machine" can use to generate s.
The W-machine (or World-machine) is a computing machine that represents the way the observer represents the world and its constraints.

Description complexity C(s) is the length of the shortest available description of s (that makes s unique).
This notion corresponds to the usual definition introduced in the years 1960 by Andrei Kolmogorov, Gregory Chaitin and Ray Solomonoff. However, we must instantiate the machine used in that definition: C(s) corresponds to the complexity of cognitive operations performed by an observer.

Note that C(s) thus depends on the cognitive model used (I recommend Michael’s Leyton generative theory of shape as a possible component of such a model).
The other restriction consists in considering, not an ideally minimal description, but the shortest one among the descriptions currently available to the observer.

We may consider C(s) as the length of a minimal program that the O-machine can use to generate s.
The O-machine (or Observation-machine) is a computing machine that can rely on all cognitive abilities and knowledge of the observer.

Caveat: The main problem when beginning with ST is that one fails to consider events, i.e. unique situations. For instance, you may think that a window is a simple object, because it is easy to describe. Indeed! But that window over there is complex, precisely because it looks like any other windows. To make it unique, I need some significant amount of information in addition to the fact that it is a window (see Conceptual Complexity).
Similarly, consider the number 131072. There is a difference between merely saying that it is a number and producing a way of distinguishing it from all other numbers. Kolmogorov complexity corresponds to the latter action. Describing a number supposes that one eventually can reconstitute all its digits (e.g. by saying that it’s 2^17).

Remark: You’re right if you think that an abnormally complex object may be unexpected. This is consistent with the above definition, as the exceptionally complex object is abnormally simple because of its being an exception (see the "Pisa Tower" effect).

Simplicity theory has been used to explain several important phenomena concerning human interest in spontaneous communication and in news (see bibliography below). More should come. Below are a few didactic examples.

Predictions: Some phenomena explained by ST

Thanks to the above definition of unexpectedness, several quantitative predictions can be made about what human beings would regard as unexpected / improbable / interesting. Some of these predictions are illustrated in the following concrete examples. Most predictions can easily been checked by common sense, and experiments with human participants clearly confirm them (Dimulescu & Dessalles 2009). Note that no alternative theory seems available to predict these same facts.

Remarkable lottery drawings (interesting structures)
The Lincoln-Kennedy effect (coincidences)
The "next door" effect (proximity)
The "Eiffel Tower" effect (simple landmarks)
The "Robert Wadlow" effect (world record)
The fish story effect (atypicality)
The running nuns (departure from norm)
The "rabid bat" effect (complex causal history)
Inverted stamps (rarity)
The "You? Here?" effect (fortuitous encounters)
The "Pisa Tower" effect (the most complex may turn out be the simplest!)
The lunar eclipse (why predicted events may still be unexpected)

And also:

Oh! Nooo! (Good luck and bad luck) ➜ read paper
This reminds me of... (Conversational topic connectedness) ➜ read paper
I recently noticed something strange... (memorability of events) ➜ read paper

Relevance

ST provides a new definition of Relevance.

Probability, Simplicity and Information

A new definition of probability

One of ST’s main claims is that unexpectedness can be used to define ex post probability, thanks to the following formula:

*Ex-post probability*
p = 2^-U

This formula indicates that human beings assess probability through complexity, not the reverse. Though the very notion of probability is dispensable in Cognitive Science, the preceding formula is important to account for the many ‘biases’ that have been noticed in human probabilistic judgment (Saillenfest & Dessalles, 2015).

See the ‘Throwing coins’ example.

Cognitive Information

ST’s formula p=2^-U looks like the converse of Claude Shannon’s definition of information. We might thus be tempted to equate unexpectedness U with information I:

I = U

This means that complexity and unexpectedness are cognitively fundamental, and that probability is, at best, a derived notion. We expect human individuals to be able to convert complexity drops into (low) probability, but not the converse (hence the impressive so-called cognitive ‘biases’ that Daniel Kahneman, Amotz Tversky and others discovered) (see Saillenfest & Dessalles, 2015).

The term of unexpectedness U allows to make several non-trivial predictions about what constitutes valuable information. These predictions include logarithmic variations with distance (see The "next door" effect), the role of prominent places or individuals (see The "Eiffel Tower" effect), habituation effects, the importance of coincidences (see The Lincoln-Kennedy effect), recency effects, transitions, violations of norms (see The running nuns), and records (see The "Robert Wadlow" effect). These theory-based predictions apply to personalized information and to newsworthiness in the media as well.

The other fundamental dimension of information is however missing: emotional intensity E. One should rather write:

I = U + E_h

Emotional intensity, Moral judgments, Responsibility

A crucial observation is that unexpectedness U controls Emotional Intensity in narratives (and beyond).

This means that emotional events elicit more intense emotions when they appear more unexpected.
This observation has far-reaching consequences. Here are a few of them.

Reported emotional intensity grows with the temporal, spatial or social proximity of the emotional event. ➜ See the Falling roof tile story.
Events elicit more intense emotions if they involve coincidences.
The feeling of near-miss or of luck is controlled by the simplicity of the causal switch between the desired and the unpleasant state of the world.
Moral judgment, action and responsibility depend on the simplicity of the causal link from action to consequences. ➜ see the Tunnel story.

Logic, independence, causality

ST provides a new definition of independence.
There are also several relations to Logic.
ST provides a new definition of mutability.

Frequently asked questions

Complexity can’t be computed. How would people have access to it?
    ST considers a resource-bounded version of Kolmogorov complexity, which is computable.
    See the Observation machine.
    Note also that probability theory relies on Set theory. But most sets considered in probabilistic reasoning are not computable
    (e.g. the set of all people who got a flu).
Some improbable objects are improbable because they are complex, not simple.
Answer in the Pisa Tower effect.
Simple situations are boring, not interesting.
Such "situations" are frequent. Each instance is complex, as you need information to discriminate it among all instances to make it an event.
See Caveat above. See also the Conceptual Complexity page.
Expected situations can still be interesting.
‘Unexpected’ does not mean ‘unpredicted’. See the Lunar Eclipse example.
It is not always clear what belongs to generation and what belongs to description.
    Depending on the predicates involved, part of the computation may migrate between
    the generation side and the description side (leaving the difference constant).
    See the Inverted Stamp example.
What’s the link with entropy?
When statistical distributions are available, unexpectedness equals cross-entropy.
Generation complexity and Description Complexity are not based on prefix-free codes. Why?
Prefix-free codes are used to communicate information.
Here, we need to use the standard definition of complexity, in which code ‘words’ are externally delimited.
With the definition of probability given by p = 2^-U, probabilities sum up to more than 1!.
    Yes, indeed. This is not a problem, as p corresponds to ex-post probability.
    For instance, two unremarkable lottery draws may both have ex-post probability close to 1.
    Only strictly ex-ante probabilities are supposed to sum to 1.

MOOC

Simplicity Theory is presented in the fifth chapter of this great MOOC on algorithmic information:

aiai.telecom-paris.fr

Contents